Edu Technology and Algebra

Sunday, November 6, 2011

Sample Test Questions - Polynomials and Their Operations

Sample 10-question Elementary Algebra test covering topics found in Chapter 5 - Polynomials and Their Operations.

1. Simplify.

${\left( {\frac{{2{x^3}}}{{3{y^2}}}} \right)^3}$

Apply the rules of exponents.

2. Simplify.

${(5x{y^{ - 3}}{z^4})^{ - 3}}$

Apply the rules of exponents.

3. Calculate f(-2) given

$f(x) = - 3{x^2} + 2x - 9$

Replace every instance of x with -2.

4. Add.

$(3{x^2} + 2x - 9) + ( - 5{x^2} - 7x + 7)$

Combine like terms.

5. Subtract.

$( - 5{x^2} - 3x + 4) - (2{x^2} - 3x - 5)$

Distribute the -1 and then combine like terms.

6. Multiply.

$- 2{x^2}(3{x^3} + 2{x^2} - 5x + 1)$

Distribute the monomial in front of the parentheses.

7. Multiply.

${(2x - 3)^3}$

Distribute and then combine like terms.

8. Divide.

$\frac{{20{x^6} + 18{x^5} - 4{x^3}}}{{2{x^3}}}$

Divide each term by the monomial in the denominator.

9. Divide.

$\frac{{3{x^4} + 4{x^3} - 13{x^2} + 9x + 3}}{{3x - 2}}$

Perform the polynomial long division.

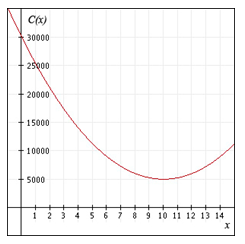
10. A projectile is fired from the top of an 80 ft building with an initial velocity of 64 feet per second. The height of the projectile in feet after t seconds is given by the following function and is graphed below.

$h(t) = - 16{t^2} + 64t + 80$

a. Use the graph to determine how long it takes to reach the maximum height.
b. Use the graph to determine how long will it take to hit the ground?
c. Use the function to determine the height of the projectile after 4 seconds?

Beginning Algebra in the Early 20th Century

Image via WikipediaIt is interesting to see how content changes and stays the same over time. Check out these two beginning Algebra books that I found on the Project Gutenberg webiste:

A First Book in Algebra by Wallace C. Boyden 1895

The First Steps in Algebra by G. A. Wentworth 1904

"162. A root which can be found exactly is called an exact or
rational root. Such roots are either whole numbers or fractions.
A root which is indicated but can be found only approxi-
mately is called a surd. Such roots involve the roots of imperfect
powers.

Rational and surd roots are together called real roots.

A root which is indicated but cannot be found, either exactly
or approximately, is called an imaginary root. Such roots in-
volve the even roots of negative numbers."

---

Saturday, November 5, 2011

Sample Test Questions - Factoring and Solving

Sample 10-question Elementary Algebra test covering topics found in Chapter 6 - Factoring and Solving by Factoring.

1. Factor.

$2{x^2} + 6x - 3xy - 9y$

Four term polynomial - factor by grouping.

2. Factor.

$6{x^2} + 25x - 9$

Three-term polynomial - factor trinomials using the trial and error technique.

3. Factor.

$2{x^6} - 128$

Two-term polynomial - first factor out the GCF. Then factor the resulting special binomial factors completely.

4. Solve.

${(x - 3)^2} = 2(5 - 3x)$

First multiply to obtain standard form, equal to zero. Then factor and set each factor equal to zero.

5. Solve.

$- 3{x^2} + 300 = 0$

Factor and then set each variable factor equal to zero.

6. Find a quadratic equation with integer coefficients that has the following solutions:

$\left\{ { - 3,\,\,\frac{2}{3}} \right\}$

Work the process for solving by factoring in reverse.

7. Given

$f(x) = 2{x^2} - 9x - 5$

a. Calculate f(0).
b. Find all values of x for which f(x) = 0.

8. The product of two consecutive positive odd integers is eleven less than 10 times the larger. Find the integers.

9. The length of a rectangle is 6 cm longer than twice its width. If the area is 140 cm^2, find the dimensions of the rectangle.

10. The cost of a particular car in dollars can be approximated by the function

$C(x) = 250{x^2} - 5,000x + 30,000$

where x represents the age of the car in years (graphed below).

a. Use the graph to determine the cost of the car when it was new?
b. Use the graph to determine how old the car will be when it reaches its minimum cost?
c. Use the function to determine how much this car will be worth when it reaches 5 years old?

Friday, November 4, 2011

Elementary Algebra (Ch.1) Real Numbers and Their Operations

Elementary Algebra is an open textbook that is available to read for free on the flatworld knowledge website. Chapter 1 is considered a review chapter covering many of the topics found in a Pre-Algebra course. You will find written examples, video examples, and exercises with answers to the odd problems.

1.1 Real Numbers and the Number Line
1.2 Adding and Subtracting Integers
1.3 Multiplying and Dividing Integers
1.4 Fractions
1.5 Review of Decimals and Percents
1.6 Exponents and Square Roots
1.7 Order of Operations

In addition, you will find a complete review exercise section and a practice test.

1.8 Review Exercises and Sample Exam

Feel free to copy and paste the links found here and post them in your LMS. Links to all of the chapters can be found by clicking the Elementary Algebra course button at the top of this page.

---

Tuesday, November 1, 2011

Solve by Factoring in Elementary Algebra

Learning how to solve equations is one of our main goals in Algebra. At this point, we know how to solve linear equations,

And now we begin to learn how to solve quadratic equations,

One way to solve quadratic equations is to use factoring and the zero-product property. The zero-product property sounds fancy but it simply states that,

So if we can factor a quadratic equation in standard form, equal to zero, we can then set each factor equal to zero and solve the resulting linear equations. For example, solve the following quadratic equation:

Step 1: Express the quadratic equation in standard form, equal to zero.

Step 2: Factor the quadratic expression.

Step 3: Apply the zero-product property and set each variable factor equal to zero.

Step 4: Solve the resulting linear equations.

The solutions are -5, and -3/2. You can check that these are solutions by substituting them into the original equation and verify that they lead to a true statement. Here is another example on video:

Hopefully you can see that the factoring step is very important in this process. Take care to factor your quadratic equations carefully because this is the step where most students make an error.

Elementary Algebra Textbook - Chapter 6 Factoring and Solving by Factoring
Elementary Algebra Textbook - Chapter 6 YouTube Playlist

---

Thursday, October 27, 2011

Factoring in Elementary Algebra

Right now we are trying to learn how to factor in our Elementary Algebra course (Algebra 1). Many students find this topic to be very difficult... but it is important to get it right because factoring is an essential skill in mathematics. For example,

The general factoring guidelines found in the free Elementary Algebra textbook offered on the Flat World Knowledge website follow:

1. Check for common factors. If the terms have common factors, then factor out the greatest common factor (GCF) and look for the resulting polynomial factors to factor further.
2. Determine the number of terms in the polynomial:

Four term polynomials are factored by grouping.
Trinomials (3 terms) are factored using “trial and error” or the AC method.
Binomials (2 terms) are factored using the following special products.

3. Look for factors that can be factored further.
4. Check by multiplying.

* If a binomial is both difference of squares and cubes, then we should factor it as difference of squares first to obtain a more complete factorization.
* Not all polynomials with integer coefficients factor, in this case, we say that the polynomial is prime.

Solution: This four term polynomial has a GCF of 3x , we factor this out first.