Currently I am working hard to get my Trigonometry content converted to mobile friendly formatting in the new content system. Lots of issues but I am making progress.
https://ens-textbooksystem.appspot.com/
http://www.opengraphingcalculator.com/
http://www.openalgebra.com/
http://www.opentrigonometry.com/
http://www.trigcheatsheet.com/
I need to plan a complete overhaul of these offerings at some point!
Edu Technology and Algebra
Exploring education technology in the 21st century.
Thursday, July 7, 2016
Sunday, September 6, 2015
HTML5 Phaser Game Framework
The Visalia GDG and COS SETA is sponsoring a friday game programming meetup/workshop using all free resources.
 For this we will use the following:
For this we will use the following:
1. Github.com to store and share our code.
2. Cloud9 online IDE. Can sign in with github and it should work in the computer lab.
3. Intel XDK for an offline IDE that can compile to any mobile device as well as HTML5.
4. Phaser 2D game programming framework.
5. Google search for help!
Friday #1 *****************************
Friday #2 *****************************
Friday #3 *****************************
Friday #4 *****************************
I had fun... thank you everyone!
List of really good resources updated as we progress:
---
1. Github.com to store and share our code.
2. Cloud9 online IDE. Can sign in with github and it should work in the computer lab.
3. Intel XDK for an offline IDE that can compile to any mobile device as well as HTML5.
4. Phaser 2D game programming framework.
5. Google search for help!
Friday #1 *****************************
- Introduction
- Goal: https://shmup-run01-johnredden.c9.io
- Free Book: https://leanpub.com/html5shootemupinanafternoon/read
- Setup of Cloud9 Online IDE (sign in with GitHub)
- Starter Template: https://github.com/bryanbibat/html5shmup-template
- Afternoon 0, 1 and start afternoon 2.
- Socialize and share game ideas.
Friday #2 *****************************
- Basic Phaser Code
- Upgrade this game together: iThrowRock
Starter Template: https://github.com/johnRedden/Rocks - Continue 1942 Game (How to make groups.)
- Socialize a bit more this time!
Friday #3 *****************************
- Sprite groups and p2 collision groups.
- Upgrade this game together iThrowRock:
Starter Template: https://github.com/johnRedden/RocksVer2 - Modify the game and share results.
Friday #4 *****************************
- Basic game from scratch. Balloon popping!
Starter Template: https://github.com/johnRedden/balloonpopV1 - Going from zero to something today!
Friday #5 *****************************
- Game States (Air Hockey)
Starter Template: https://github.com/johnRedden/AirHockey - APK files for Android
- Certificates signed by the President.
List of really good resources updated as we progress:
- Javascript Objects w3schools
- Phaser Documentation
- Phaser Examples
- Extra examples (Phaser Labs)
- Phaser Cheat Sheet
---
Labels:
phaser,
programming,
tutorial
Monday, July 13, 2015
Open Graphing Calculator
Here is the link to our pre-Beta release of the Open Graphing Calculator. The current alpha version is 0.35 and I plan on updating it every Sunday...we are fixing issues as they arise. So hit [ refresh ] often.
Be sure to play around with the calculus toggle buttons. Report any issues on gitHub.
Be sure to play around with the calculus toggle buttons. Report any issues on gitHub.
Labels:
calculator,
graph,
graphing,
open
Tuesday, April 21, 2015
Free Printable Lined Graph Paper
Free printable 8.5 in. by 11 in. papers in PDF or Docx formats.
* The word templates were made by inserting a lined image as a watermark.
Dots every 0.25 inch, used for graphing.
Squares 0.2 inch, perfect for graphing.
* The word templates were made by inserting a lined image as a watermark.
Saturday, May 10, 2014
Free Trigonometry Site
 I'm feeling good about our new free Trigonometry website. It's just a Blogger site, but it's getting good reviews. Today I added some big mobile friendly buttons.
I'm feeling good about our new free Trigonometry website. It's just a Blogger site, but it's getting good reviews. Today I added some big mobile friendly buttons.A www.merlot.org editor gave it a good rating. So check it out and feel free to send me any suggestions.
Also, since it is a Blogger site, you can cut and paste anything you find there into our course management system. Like so:
Copy-and-paste easy... I really like that.
Labels:
cheat sheet,
free help,
graphs,
interactive,
math,
math help,
mathematics,
trig,
trigonometry
Friday, December 13, 2013
Trigonometry 101
 This semester I ran a partially flipped open source Trigonometry course using a free textbook and youTube videos. To give back to the OER community, I have recreated my blackboard shell here in a single blog post. I am offering all of the worksheets that I have created below in PDF and source DOCX format under a creative commons license (cc-by-sa). Please feel free to copy anything here, modify, and/or redistribute.
This semester I ran a partially flipped open source Trigonometry course using a free textbook and youTube videos. To give back to the OER community, I have recreated my blackboard shell here in a single blog post. I am offering all of the worksheets that I have created below in PDF and source DOCX format under a creative commons license (cc-by-sa). Please feel free to copy anything here, modify, and/or redistribute.Open Textbook: Trigonometry by Michael Corral
Videos: Mathispower4u Trigonometry by James Sousa
End-page Formulas (Trig. cheat sheet): [ Trigonometry Definitions and Formulas | source ]
Free Graphing Utility: Desmos.com
Free CAS: WolframAlfa
Chapter 1: Right Triangle Trigonometry
1.1 Angles: [ Assignment 1a : source ]Video notes: Angle Basics
Video notes: Degrees, Minutes, and Seconds
Video notes: Angle Relationships and Types of Triangles
Video notes: The Pythagorean Theorem
Video notes: Converse of the Pythagorean Theorem
1.2 Trigonometric Functions: [ Assignment 1b : source ]
Video Notes: Introduction to Trigonometric Functions
Video Example: Determine Trigonometric Function Values
Video Example: Trig. Function Values with Hypotenuse Missing
1.3 Applications: [ Assignment 1c : source ] [ Assignment 1d : source ]
Video Example: Determine the Length of a Side
Video Example: Perimeter of an Equilateral Triangle
1.4 Trigonometric Functions of any Angle: [ Assignment 1e : source ]
Video Examples: Determine the Reference Angle
Video Notes: Introduction to Trig Functions using Angles
1.5 Rotations and Reflections: [ Assignment 1f : source ]
*** *** *** [ Sample Exam #1 | source ] *** *** ***
Chapter 2: General Triangles
2.1 Law of Sines [ Assignment 2a | source ]Video: The Law of Sines: The Basics
Video: The Law of Sines: The Ambiguous Case
Example: Solve a Triangle Using the Law of Sines
2.2 Law of Cosines [ Assignment 2b | source ]
Video: The Law of Cosines
Example: Application of the Law of Cosines
Example: Determine an Angle given SSS
2.3 Law of Tangents
2.4 Area of a Triangle [ Assignment 2c | source ]
Example: Determine the Area of a Triangle Using the Sine Function
Example: Area using Heron's Formula
Chapter 3: Identities
3.1 Basic Identities [ Assignment 3a | source ]Video: Fundamental Identities
Video: Verifying Identities (good using a slightly different method.)
3.2 Sum and Difference Formulas [ Assignment 3b | source ]
Video: Sum and Difference Identities for Cosine
Video: Sum and Difference Identities for Sine
Video: Sum and Difference Identities for Tangent
3.3 Double and Half-Angle Formulas [ Assignment 3c | source ]
Video: Double Angle Identities
Example: Double Angle Example Given Information
Example: Using the Half Angle Formula (use degrees here)
Example: Using Sine of a Half Angle
*** *** *** [ Sample Exam #2 | source ] *** *** ***
Chapter 4: Radian Measure
4.1 Radian Measure [ Assignment 4a | source ]Lecture: Radian Measure (Great video!)
4.2 Arc Length [ Assignment 4b | source ]
Lecture: Arc Length and Area of a Sector
4.3 Area of a Sector [ Assignment 4c | source ]
Lecture: Arc Length and Area of a Sector
4.4 Circular Motion [ Assignment 4d | source ]
Lecture: Linear Velocity and Angular Velocity
Chapter 5: Graphing and Inverse Functions
5.1 Graphing Trigonometric Functions [ Assignment 5a | source ]Video Lecture: Graphing the Sine and Cosine Function
Video Lecture: Graphing the Tangent Function
Video Lecture: Graphing Cosecant and Secant
5.2 Properties of Graphs[ Assignment 5b | source ]
Video Lecture: Amplitude and period of Sine and Cosine
Video Lecture: Horizontal and Vertical Translations of Sine and Cosine
Video Lecture: Graphing Sine and Cosine with Transformations
5.3 Inverse Trigonometric Functions [ Assignment 5c | source ]
Video Lecture: Inverse Functions
Video Lecture: Intro. to Inverse Sine, Cosine, and Tangent
Video Examples: Evaluating Expressions involving the Inverse Trig. Functions
*** *** *** [ Sample Exam #3 | source ] *** *** ***
Chapter 6: Additional Topics
6.1 Solving Trigonometric Equations[ Assignment 6a | source ] [ Assignment 6b | source ] [ Assignment 6c | source ]
Video Lecture: Solving Trigonometric Equations I (Excellent introduction! Linear)
Video Lecture: Solving Trigonometric Equations II (Quadratic examples)
Video Lecture: Solving Trigonometric Equations III (Using Identities first, quadratic formula)
Video Lecture: Solving Trigonometric Equations IV (Half and multiple angles)
6.2 Numerical Methods in Trigonometry
6.3 Complex Numbers [ Assignment 6d | source ]
Video Lecture: Introduction to Complex Numbers
Video Lecture: Complex Number Operations
Video Lecture: Trigonometric Form of Complex Numbers
Video Lecture: De Moivre's Theorem
Video Lecture: Nth Roots of a Complex Number
6.4 Polar Coordinates [ Assignment 6e | source ]
Video Lecture: Introduction to Polar Coordinates
Video Lecture: Converting Polar Equations to Rectangular Equations (sound is bad)
Video Lecture: Graphing Polar Equations Part I
Video Lecture: Graphing Polar Equations Part II
*** *** *** [ Sample Exam #4 | source ] *** *** ***
*** Sample Final Exam - coming soon ***

Trigonometry 101 by John Redden is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. ---
Labels:
math,
mathematics,
mooc,
OER,
trig,
trigonometry,
worksheet
Monday, October 14, 2013
The Graphs of the Six Trigonometric Functions
The objective here is to have the basic graphs of all six trigonometric functions ready to go. Here is a link to a one-page printable reference sheet.
1. One period graphed for the sine function. ( y = sin x )
2. One period graphed for the cosine function. ( y = cos x )
Notice that cosine function is a horizontal translation of sine by π/2 units. To see this click on the link below for an interactive graph.
3. One period graphed for the cosecant function. ( y = csc x = 1 / sin x )
4. One period graphed for the secant function. ( y = sec x = 1 / cos x )
Notice that the zeros of sine and cosine define vertical asymptotes for the cosecant and secant functions. To see this click on the link below for an interactive graph.
5. One period graphed for the tangent function. ( y = tan x = sin x / cos x )
6. One period graphed for the cotangent function. ( y = cot x = cos x / sin x )
Notice that for the tangent function, the zeros of cosine determine the vertical asymptotes. And for the cotangent function, the zeros of sine determine the vertical asymptotes.
Enjoy.
1. One period graphed for the sine function. ( y = sin x )
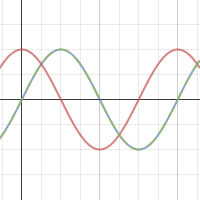 |
| Desmos Interactive Graph |
4. One period graphed for the secant function. ( y = sec x = 1 / cos x )
Notice that the zeros of sine and cosine define vertical asymptotes for the cosecant and secant functions. To see this click on the link below for an interactive graph.
 |
| Desmos Interactive Graph |
6. One period graphed for the cotangent function. ( y = cot x = cos x / sin x )
Notice that for the tangent function, the zeros of cosine determine the vertical asymptotes. And for the cotangent function, the zeros of sine determine the vertical asymptotes.
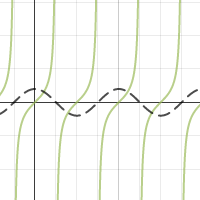 |
| Desmos Interactive Graph |
Subscribe to:
Posts (Atom)











