Math != Calculating

This is an interesting talk:



Math >> Calculating

1. Pose the right questions.
2. Real world problem --> math formulation
3. Computation
4. Math formulation --> real world problem and verification

Maybe not spend so much time on step 3?  Use computer programming to nail down understanding!  These are very interesting ideas.

===

Adding and Subtracting Rational Expressions

To simplify a rational expression:
Step 1:  Factor all denominators as a means to easily determine the LCD.
Step 2:  Multiply by the appropriate factors to obtain equivalent terms with a common denominator. 
Step 3:  Add or subtract the numerators and place the result over the common denominator. 
Step 4:  Simplify the resulting algebraic fraction.



A more involved example follows:

It is always a good idea to state the restrictions.  Remember that the restrictions are the values that produce zero in the denominator.

---

Mandelbrot Explorer using Flash

Give the below flash movie a minute to download. Move the looking glass over the picture and release it to zoom.



The orbit is displayed, real time, in the corner.

Trigonometric Function Explorer using Flash

Above you should see a flash movie that I have made.  This is a test post to see if I could emed a flash component into blogger.  The swf file has been saved in Google docs and shared with everyone. Success!

Top 100 Most Influential People of the Last Millennium

 From the economicexpert.com

 On October 10, 1999, the American cable network A&E started counting down a list of the 100 most influential people of the millennium compiled by a staff of 360 journalists, scientists, theologians, historians, and scholars.
As many as 250 people were chosen to be on the list, but only 100 made it, these are the 100 people that did the most to shape the world we live in today.

1 The List

1. Johann Gutenberg
2. Isaac Newton
3. Martin Luther
4. Charles Darwin
5. William Shakespeare
6. Christopher Columbus
7. Karl Marx
8. Albert Einstein
9. Nicolaus Copernicus
10. Galileo Galilei
11. Leonardo da Vinci
12. Sigmund Freud
13. Louis Pasteur
14. Thomas Edison
15. Thomas Jefferson
16. Adolf Hitler
17. Mahatma Gandhi
18. John LockeJ
19. Michelangelo
20. Adam Smith
21. George Washington
22. Genghis Khan
23. Abraham Lincoln
24. St. Thomas Aquinas
25. James Watt
26. Wolfgang Amadeus Mozart
27. Napoleon Bonaparte
28. Johann Sebastian Bach
29. Henry Ford
30. Ludwig van Beethoven
31. James Watson & Francis Crick
32. René Descartes
33. Martin Luther King, Jr.
34. Jean-Jacques Rousseau
35. Vladimir Lenin
36. Alexander Fleming
37. Voltaire
38. Sir Francis Bacon
39. Dante Alighieri
40. The Wright brothers
41. Bill Gates
42. Gregor Mendel
43. Mao Zedong
44. Alexander Graham Bell
45. William the Conqueror
46. Niccolo Machiavelli
47. Charles Babbage
48. Mary Wollstonecraft
49. Mikhail Gorbachev
50. Margaret Sanger
51. Edward Jenner
52. Winston Churchill
53. Marie Curie
54. Marco Polo
55. Ferdinand Magellan
56. Elizabeth Stanton
57. Elvis Presley
58. Joan of Arc
59. Immanuel Kant
60. Franklin Delano Roosevelt
61. Michael Faraday
62. Walt Disney
63. Jane Austen
64. Pablo Picasso
65. Werner Heisenberg
66. D.W. Griffith
67. Vladimir Zworykin
68. Benjamin Franklin
69. William Harvey
70. Pope Gregory VII (the oldest person on the list)
71. Harriet Tubman
72. Simón Bolívar
73. Diana, Princess of Wales (youngest on the list)
74. Enrico Fermi
75. Gregory Pincus
76. The Beatles
77. Thomas Hobbes
78. Queen Isabella
79. Joseph Stalin
80. Queen Elizabeth I
81. Nelson Mandela
82. Niels Bohr
83. Peter the Great
84. Guglielmo Marconi
85. Ronald Reagan
86. James Joyce
87. Rachel Carson
88. J. Robert Oppenheimer
89. Susan B. Anthony
90. Louis Daguerre
91. Steven Spielberg
92. Florence Nightingale
93. Eleanor Roosevelt
94. Patient Zero
95. Charlie Chaplin
96. Enrico Caruso
97. Jonas Salk
98. Louis Armstrong
99. Vasco da Gama
100. Suleiman I

NASA Photo Archive

A great resource for historical images found on Flickr:     NASA on The Common photostream:

A Delta II rocket.

More images can be found here:  NASA Images

---

Average Mathematics Scores by Country 2007

This does not seem so bad to me.  Here is the original link. 

Table 1. Average mathematics scores of fourth- and eighth-grade students, by country: 2007

Grade four		Grade eight
Country	Average score	Country	Average score
TIMSS scale average	500	TIMSS scale average	500
Hong Kong SAR1	607	Chinese Taipei	598
Singapore	599	Korea, Rep. of	597
Chinese Taipei	576	Singapore	593
Japan	568	Hong Kong SAR1, 4	572
Kazakhstan2	549	Japan	570
Russian Federation	544	Hungary	517
England	541	England4	513
Latvia2	537	Russian Federation	512
Netherlands3	535	United States4, 5	508
Lithuania2	530	Lithuania2	506
United States4, 5	529	Czech Republic	504
Germany	525	Slovenia	501
Denmark4	523	Armenia	499
Australia	516	Australia	496
Hungary	510	Sweden	491
Italy	507	Malta	488
Austria	505	Scotland4	487
Sweden	503	Serbia2, 5	486
Slovenia	502	Italy	480
Armenia	500	Malaysia	474
Slovak Republic	496	Norway	469
Scotland4	494	Cyprus	465
New Zealand	492	Bulgaria	464
Czech Republic	486	Israel7	463
Norway	473	Ukraine	462
Ukraine	469	Romania	461
Georgia2	438	Bosnia and Herzegovina	456
Iran, Islamic Rep. of	402	Lebanon	449
Algeria	378	Thailand	441
Colombia	355	Turkey	432
Morocco	341	Jordan	427
El Salvador	330	Tunisia	420
Tunisia	327	Georgia2	410
Kuwait6	316	Iran, Islamic Rep. of	403
Qatar	296	Bahrain	398
Yemen	224	Indonesia	397
		Syrian Arab Republic	395
		Egypt	391
		Algeria	387
		Colombia	380
		Oman	372
		Palestinian Nat'l Auth.	367
		Botswana	364
		Kuwait6	354
		El Salvador	340
		Saudi Arabia	329
		Ghana	309
		Qatar	307

---

Average score is higher than the U.S. average score (p < .05)
Average score is not measurably different from the U.S. average score (p < .05)
Average score is lower than the U.S. average score (p < .05)
¹ Hong Kong is a Special Administrative Region (SAR) of the People's Republic of China.
² National Target Population does not include all of the International Target Population defined by the Trends in International Mathematics and Science Study (TIMSS).
³ Nearly satisfied guidelines for sample participation rates only after substitute schools were included.
⁴ Met guidelines for sample participation rates only after substitute schools were included.
⁵ National Defined Population covers 90 percent to 95 percent of National Target Population.
⁶ Kuwait tested the same cohort of students as other countries, but later in 2007, at the beginning of the next school year.
⁷ National Defined Population covers less than 90 percent of National Target Population (but at least 77 percent).
NOTE: Countries are ordered by 2007 average score. The tests for significance take into account the standard error for the reported difference. Thus, a small difference between the United States and one country may be significant while a large difference between the United States and another country may not be significant. The standard errors of the estimates are shown in tables E-1 and E-2 available at http://nces.ed.gov/pubsearch/pubsinfo.asp?pubid=2009001.
SOURCE: International Association for the Evaluation of Educational Achievement (IEA), Trends in International Mathematics and Science Study (TIMSS), 2007.

My Very Own Channel!

I have a youTube channel now! 

http://www.youtube.com/user/johnreddenVML

---

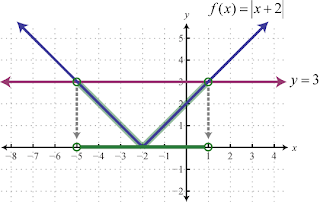
Absolute Value Inequality: A Graphical Approach

An absolute value inequality, such as,

can be solved as follows:

We can visualize these solutions if we graph the function,

in the rectangular coordinate plane and determine where the graph lies below the horizontal line given by .  In other words, for what x-values is

This idea is illustrated below:

Furthermore, we could use the same graph to visualize the solutions to,

We can see that the solutions are,

Now take the time to compare this visualization to that given on Wolfram Alpha.  Remember, it is always helpful to understand the geometric interpretation whenever possible.

Goofram - Search Google and Wolfram Alpha at the same time!

This is an interesting idea... google and Alpha side by side!

Goofram - Search Google and Wolfram Alpha at the same time!

---

Math Education in the Real World

Here is a nice talk... "students come pre-installed with viruses..."

The Future of the Lecture?

Here is a link that I found interesting regarding the future of education.

A Parody of the Future of Education




It is worth thinking about.

CAUTION: Multiplication before addition or subtraction.

Be aware that "they" like to dangle addition or subtraction in front of us like follows:

5 - 2(x + 7) = 11

It is very much tempting to subtract 5 - 2, isn't it? DO NOT DO IT... the order of operations requires that we multiply (or distribute) before subtraction. The solution follows:

Screen Capture

Use the Snipping Tool in Windows Vista for quick and easy screen captures. It is included, so to find it click the Start menu and type "snipping" in the search box.

Here is a link to more detailed instructions.

Solving Linear Equations

Another video posted on YouTube. It seems that YouTube is more mobile friendly than blip. Here is another video test.

Stop Motion Tutorial

This is my first attempt at a stop motion video tutorial. Just a test really. I am solving a linear equation that happens to be an identity.

Free Fonts

Links to free fonts and how to make them! This might be useful.

http://www.articulate.com/rapid-elearning/over-100-free-handwritten-fonts/

A brief history of everything...

I really like this idea.

Copyrights Made Easy

The creative commons website offers easy to use tools for determining which attribution is best for you. Visit the site:

http://creativecommons.org/

Click license, and after answering the questions click the Select a License button. It then shows which license is best and provides HTML that can be cut-and-pasted into your website as follows:


This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 United States License.

Free Digital Textbook Initiative Review Results

The California Learning Resource Network reviewed several free textbooks and compared the content to the current California content standards.  Have a look:

Free Digital Textbook Initiative Review Results